lawyerslobi.blogg.se - Sigma math calc

#Sigma math calc series#

In this course, we don’t derive the formula to add together the square numbers. In this case, the number of terms is 10 and. We read here that the formula to sum the first terms of a geometric sequence is Now that we have established, let’s find the first term in this summation and the last term, so that we can use the other formula for summing an arithmetic sequence which isĪ geometric sequence has general term. (Calculate: We ‘ ‘ because the 7th term is included). In this example, our sequence is still arithmetic, however we are beginning at the 7th term and finishing at the 20th term.

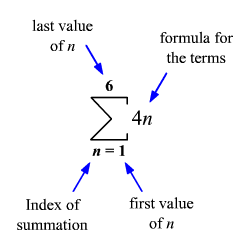
Try typing example 1 into this sigma calculator. It is clear that having a formula offers a significant advantage over writing out all the terms and adding them together. The sequence has first term and common difference. In this case, the sequence is arithmetic, and so we can calculate the sum of the first 100 terms using the formula for arithmetic series: where is the first term and is the common difference.

#Sigma math calc series#

Using formulae Example 1 Arithmetic Series

Use a scientific calculator, or an online sigma calculator.

If you know a formula for the kind of sequence, use the formula.

Write out all the terms and add them together.

There are three ways to calculate the value of (evaluate) a sum represented with sigma notation. We can also understand this notation as representing the number or expression which the sum is equal to. It reads ‘sum the terms of the sequence starting at and ending at. Is the instruction to add together the first five terms of the sequence. Sigma notation is used to hold all the terms of a series on one small space on a page.